|
Es
decir, que si representa una función periódica de periodo
T=2p /w podemos expresar la función mediante un desarrollo en serie
de la forma:
.gif)
Siendo A0, A1,
A2,.... las amplitudes; w,
2w, 3w,...las frecuencias,
y j1, j2, j3,...
las fases iniciales de las funciones armónicas simples componentes
(algunas de las cuales podrán ser nulas). En general el número
de términos del desarrollo de Fourier necesarios para representar
una función es infinito pero muchas veces las amplitudes Ai decrecen
muy rápidamente, por lo que el desarrollo puede reducirse a unos
pocos términos.
El término constante A0
carece de interés en acústica, por no llevar asociado ningún
cambio de presión. El término de menor frecuencia, esto
es,
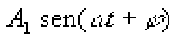
tiene
un periodo idéntico al de la vibración compuesta y recibe
el nombre de vibración fundamental o primer armónico.
Los demás términos corresponden a los armónicos superiores
y tienen frecuencias que son múltiplos de la fundamental.
Se llama espectro acústico de un sonido compuesto a una
representación de las amplitudes o de las intensidades relativas
frente a las frecuencias de las ondas sonoras simples que lo componen.
 

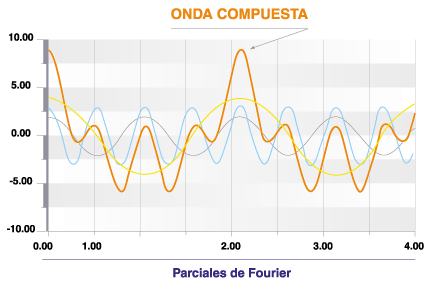
 
El
Timbre de un sonido compuesto está definido por su espectro de frecuencias,
y es la cualidad.
El oído no responde igual a todas las frecuencias, sino que lo hace
a un conjunto de ellas, por esto cuando se hace el análisis espectral
de la señal acústica dividimos todo el conjunto en Bandas
de Frecuencia.
|

